Question

已知抛物线y=ax²+bx+c通过点(1,1),且在?点(2,-1)?处与直线y=x-3相切,求a、b、c的值.

Answer 1

分析:题中涉及三个未知量,已知中有三个独立条件,因此,要通过解方程组来确定a、b、c的值.

解:因为y=ax²+bx+c过点(1,1),

所以a+b+c=1.

y′=2ax+b,曲线过点(2,-1)的切线的斜率为4a+b=1.

又曲线过点(2,-1),所以4a+2b+c=-1.

由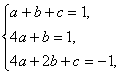解得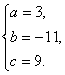所以a、b、c的值分别为3、-11、9.

点评:本题主要考查了导数的几何意义、导数的运算法则及运算能力.解决问题的关键在于理解题意、转化条件和结论,将两者统一起来.