题目内容
9.二项式(x+$\frac{1}{x}$)4展开式中的常数项是20.分析 根据二项式(x+$\frac{1}{x}$)4展开式的通项公式,令x的指数等于0,求出对应展开式的常数项.
解答 解:二项式(x+$\frac{1}{x}$)4展开式的通项公式为:
Tr+1=${C}_{4}^{r}$•x4-r•${(\frac{1}{x})}^{r}$=${C}_{4}^{r}$•x4-2r,
令4-2r=0,解得r=2;
所以展开式的常数项为${C}_{4}^{2}$=6.
故答案为:6.
点评 本题考查了利用二项式展开式的通项公式求展开式中特定项的应用问题,是基础题目.

练习册系列答案
相关题目
19.若纯虚数z满足iz=1+ai,则实数a=( )
| A. | 0 | B. | -1或1 | C. | -1 | D. | 1 |
20.函数$f(x)=3sin(2x-\frac{π}{3}+ϕ),ϕ∈(0,π)$满足f(|x|)=f(x),则ϕ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
17.执行如图所示程序图,若N=7时,则输出的结果S的值为( )
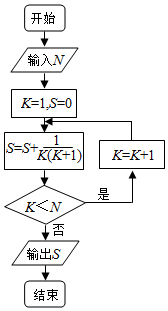

| A. | $\frac{8}{7}$ | B. | $\frac{6}{5}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{6}$ |
1.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,若点F关于双曲线的渐近线的对称点在双曲线的右支上,则该双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |