题目内容
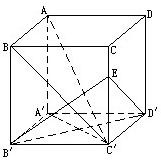 在长方体AC′中,AB=AC=a,BB′=b(b>a),连接BC′,过点B′作B′E⊥BC′交CC′于E.
在长方体AC′中,AB=AC=a,BB′=b(b>a),连接BC′,过点B′作B′E⊥BC′交CC′于E.(1)求证:AC′⊥平面EB′D′;
(2)求三棱锥C′-B′D′E的体积.
分析:(1)欲证AC′⊥平面EB′D′,根据直线与平面垂直的判定定理可知只需证AC′与平面EB′D′内两相交直线垂直,而AC′⊥B′D′,AC′⊥B′E,满足定理条件;
(2)要求三棱锥C′-B′D′E的体积,可转化成求三棱锥E-B′D′C'的体积,根据B′E⊥BC′求出EC',根据三棱锥的体积公式进行求解即可.
(2)要求三棱锥C′-B′D′E的体积,可转化成求三棱锥E-B′D′C'的体积,根据B′E⊥BC′求出EC',根据三棱锥的体积公式进行求解即可.
解答:(1)证明:由题意,长方体底面为正方形,
A′C′⊥B′D′,AC′⊥B′D′,
又∵B′E⊥BC′,
∴AC′⊥B′E,
∴AC′⊥平面EB′D′
(2)解:由∠B′C′B=∠B′EC′,又EC′=
=
.
∴VC′-B′D′E=VE-B′C′D′=
×
a2×
=
A′C′⊥B′D′,AC′⊥B′D′,
又∵B′E⊥BC′,
∴AC′⊥B′E,
∴AC′⊥平面EB′D′
(2)解:由∠B′C′B=∠B′EC′,又EC′=
| a |
| tan∠B′EC′ |
| a2 |
| b |
∴VC′-B′D′E=VE-B′C′D′=
| 1 |
| 3 |
| 1 |
| 2 |
| a2 |
| b |
| a4 |
| 6b |
点评:本题主要考查了直线与平面垂直的判定,以及棱柱、棱锥、棱台的体积,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
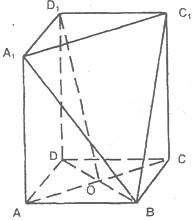 在长方体ABCD-A1B1C1D1中,AB=BC=2,O为AC和BD的交点,过A、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-AC1Dl,且这个几何体的体积为.
在长方体ABCD-A1B1C1D1中,AB=BC=2,O为AC和BD的交点,过A、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-AC1Dl,且这个几何体的体积为. 如图,在长方体ABCD-A1B1C1D1中,
如图,在长方体ABCD-A1B1C1D1中, (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.