Question

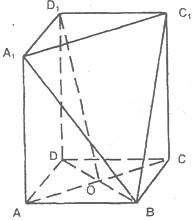在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，O为AC和BD的交点，过A、C₁、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-AC₁D_l，且这个几何体的体积为．
（1）求证：OD₁∥平面BA₁C₁
（2）求棱A₁A的长：
（3）求点D₁到平面BA₁C₁的距离．

Answer 1

分析：（1）欲证OD_l∥平面BA₁C₁，根据直线与平面平行的判定定理可知只需证OD_l与平面BA₁C₁内一直线平行，取A₁C₁的中点M，连接BM，MD₁，易证四边形OBMD₁是平行四边形，则OD₁∥BM，BM?平面BA₁C₁，满足定理所需条件；
（2）没A₁A=h，由题意可知VABCD-A1C1D1=

V	ABCD-A1B1C1D1

-VB-A1B1C1=10建立等式关系，求出所求即可；
（3）点D₁到平面BA₁C₁的距离即为点B₁到平面BA₁C₁的距离d，根据VB1-BA1C1=VABCD-A1B1C1D1-10建立等式关系解之即可求出点D₁到平面BA₁C₁的距离．

解答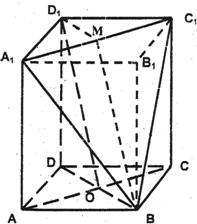：解：（1）证明：取A₁C₁的中点M，连接BM，MD₁，则MD1

∥ .

.

BO
所以四边形OBMD₁是平行四边形，OD₁∥BM
又BM?平面BA₁C₁
∴OD_l∥平面BA₁C₁（4分）
（2）设A₁A=h，由题设可知VABCD-A1C1D1=

V	ABCD-A1B1C1D1

-VB-A1B1C1=10（6分）
得SABCD×h-

1

3

×S△A1B1C1×h=10，即2×2×h-

1

3

ו

1

• 2

×2×2×h=10
解得h=3
棱A₁A的长为3（10分）
（3）点D₁到平面BA₁C₁的距离即为点B₁到平面BA₁C₁的距离d．B!M=

2

，BM=

B B 2 1 • + B1．M2

=

32+( 2 )2

．=

11

∴SBA1C1=

1

2

×A1C]×BM=

1

2

×2

2

×

11

=

22

（12分）
又VB1-BA1C1=VABCD-A1B1C1D1-10

1

3

SBA.1C1d=2×2×3-10=2
∴

1

3

×

22

×d=2∴d=

3 22

11

点D₁到平面BA₁C₁的距离

3 22

11

（14分）

点评：本题主要考查了线面平行的判定，以及利用体积法求高和点到平面的距离的度量，同时考查了空间想象能力、计算能力、转化与划归的思想，属于中档题．