题目内容
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,则此球的体积为
,则此球的体积为
A. π π | B.4 π π | C.4 π π | D.6 π π |
B
解析试题分析:因为平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为 ,
,
所以球的半径为: .所以球的体积为:
.所以球的体积为: =4
=4 π故选B.
π故选B.
考点:本题主要考查球的截面性质定理,球的体积计算公式。
点评:简单题,立体几何问题,注意几何图形,并将空间问题转化成平面问题。

练习册系列答案
相关题目
某几何体的三视图如下图所示,则该几何体为( )
| A.三棱柱 | B.三棱锥 | C.圆锥 | D.四棱锥 |
某几何体的三视图如图,则该几何体的表面积为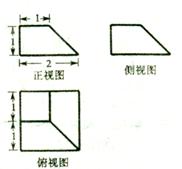
A. | B. |
C. | D. |
在正方体 中,
中, 是棱
是棱 的中点,
的中点, 是侧面
是侧面 内的动点,且
内的动点,且 平面
平面 ,则
,则 与平面
与平面 所成角的正切值构成的集合是( )
所成角的正切值构成的集合是( )
A. | B. | C. | D. |
有一个几何体的三视图如图所示,则该几何体的体积为
| A.16 | B.20 | C.24 | D.32 |
一个空间几何体的三视图如图所示,则该几何体的表面积为( )
A. | B. | C. | D. |






