Question

过抛物线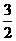(t为参数)的焦点的弦长为2，则该弦所在直线的倾斜角为（　　）

A.

B.或

C.

D.或

Answer 1

解析一：将抛物线的参数方程化成普通方程为y²=x,它的焦点为（，0）.

设弦所在直线的方程为y=k(x-).

由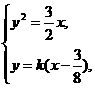消去y，得64k²x²-48(k²+2)x+9k²=0,

设弦的两端点坐标为（x₁,y₁）、(x₂,y₂),

则|x₁-x₂|=

=

=

=

∵

∴=2.

∴k²=3,k=±.

∴直线的倾斜角为.

解析二：由抛物线的参数方程得y²=x,它的焦点为（，0）.

设弦所在直线的参数方程为(m为参数)，代入y²=x,得m²sin²α-cosα·m-=0.

∴=4，

即9cos²α+9sin²α=16sin⁴α.

∴sin⁴α=,sin²α=34,sinα=±.

∴α=或α=.

答案：B