题目内容
设函数f(x)的定义域关于原点对称,且满足①f(x1-x2)=
;②存在正常实数a,使f(a)=1.求证:
(1)f(x)是奇函数;
(2)f(x)是周期函数,并且有一个周期为4a.
| f(x1)f(x2)+1 |
| f(x2)-f(x1) |
(1)f(x)是奇函数;
(2)f(x)是周期函数,并且有一个周期为4a.
考点:抽象函数及其应用,函数奇偶性的判断,函数的周期性
专题:函数的性质及应用
分析:(1)将x1-x2和x2-x1分别代入抽象表达式①,即可判断f(x1-x2)与f(x2-x1)之间互为相反数,并推断函数f(x)为奇函数.
(2)根据条件f(a)=1,结合抽象函数的关系以及周期的定义进行推导即可.
(2)根据条件f(a)=1,结合抽象函数的关系以及周期的定义进行推导即可.
解答:
解:(1)不妨令x=x1-x2,
则f(-x)=f(x2-x1)=
=-
=-f(x1-x2)=-f(x),
∴f(x)是奇函数;
(2)若f(a)=1,则f(-a)=-1,
f(x-a)=
=
,
则f(x-2a)=f(x-a-a)=
=
=
=-
,
即 f(x-4a)=f(x-2a-2a)=-
=f(x),
∴f(x-4a)=f(x),
∴f(x)是周期函数,4a是一个周期.
则f(-x)=f(x2-x1)=
| f(x2)f(x1)+1 |
| f(x1)-f(x2) |
| f(x1)f(x2)+1 |
| f(x2)-f(x1) |
∴f(x)是奇函数;
(2)若f(a)=1,则f(-a)=-1,
f(x-a)=
| f(x)f(a)+1 |
| f(a)-f(x) |
| f(x)+1 |
| 1-f(x) |
则f(x-2a)=f(x-a-a)=
| f(x-a)+1 |
| 1-f(x-a) |
| ||
1-
|
| f(x)+1+1-f(x) |
| 1-f(x)-f(x)-1 |
| 1 |
| f(x) |
即 f(x-4a)=f(x-2a-2a)=-
| 1 |
| f(x-2a) |
∴f(x-4a)=f(x),
∴f(x)是周期函数,4a是一个周期.
点评:本题主要考查抽象函数的应用以及函数奇偶性和周期性的判断和求解,利用定义是解决本题的关键.

练习册系列答案
相关题目
复数z=
(i是虚数单位)的共轭复数为( )
| 5i |
| (2-i)(2+i) |
| A、i | ||
| B、-i | ||
C、
| ||
D、-
|
已知f(cosx)=cos17x,则f(sinx)的结果是( )
| A、sin17x | ||
| B、cos17x | ||
C、sin
| ||
D、cos
|
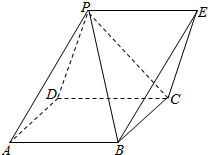 有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起,得到一个如图所示的多面体;
有一个所有棱长均为a的正四棱锥P-ABCD,还有一个所有棱长均为a的正三棱锥,将此三棱锥的一个面与正四棱锥的一个侧面完全重合的黏在一起,得到一个如图所示的多面体;