Question

【题目】已知数列、满足，，其中，则称为的“生成数列”．

（1）若数列的“生成数列”是，求；

（2）若为偶数，且的“生成数列”是，证明：的“生成数列”是；

（3）若为奇数，且的“生成数列”是，的“生成数列”是，…，依次将数列，，，…的第项取出，构成数列．

探究：数列是否为等比数列，并说明理由．

Answer 1

【答案】（1）；（2）见解析；（3）见解析

【解析】

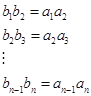试题（1）解：，，同理，；（2）只需按照定义证明即可，证明：，∵为偶数，将上述个等式中第2，4，6， ，这个式子两边取倒数，再将这个式子相乘得： ，因为，，所以根据“生成数列”的定义，数列是数列的“生成数列”；（3）因为，所以．

所以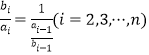欲证成等差数列，只需证明成等差数列即可．

试题解析：（1）解：，

同理，． 4分

（写对一个得1分，总分4分）

（2）证明：

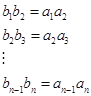7分

∵为偶数，将上述个等式中第2，4，6， ，这个式子两边取倒数，再将这个式子相乘得：

∴9分

因为，

所以根据“生成数列”的定义，数列是数列的“生成数列”． 10分

（3）证明：因为，

所以．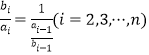

所以欲证成等差数列，只需证明成等差数列即可． 12分

对于数列及其“生成数列”

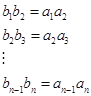
∵为奇数，将上述个等式中第2，4，6， ，这个式子两边取倒数，再将这个式子相乘得：

∴

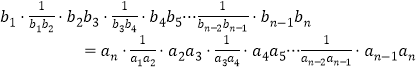
因为，

数列的“生成数列”为，因为

所以成对比数列．

同理可证，也成等比数列．即是等比数列．

所以成等差数列． 16分