题目内容
已知圆的极坐标方程为ρ=2sinθ-4cosθ,圆心为C,直线l的参数方程为:
(t为参数),且直线l过圆心C,则a为
|
-2
-2
.分析:把圆的极坐标方程化为直角坐标方程,求出圆心坐标,再利用两式相加消去t将直线的参数方程化成普通方程,由于直线l过圆心C,故圆心坐标满足直线方程,解出a即可.
解答:解:∵圆的极坐标方程是ρ=2sinθ-4cosθ,
即ρ2=2ρsinθ-4ρcosθ,
则该圆直角坐标方程为x2+y2=2y-4x,
即(x+2)2+(y-1)2=5,
表示以A(-2,1)为圆心的圆,
直线l的参数方程为:
(t为参数),
∴直线的普通方程为x+y-a-1=0,
由于直线l过圆心C,则-2+1-a-1=0
解得a=-2
故答案为:-2
即ρ2=2ρsinθ-4ρcosθ,
则该圆直角坐标方程为x2+y2=2y-4x,
即(x+2)2+(y-1)2=5,
表示以A(-2,1)为圆心的圆,
直线l的参数方程为:
|
∴直线的普通方程为x+y-a-1=0,
由于直线l过圆心C,则-2+1-a-1=0
解得a=-2
故答案为:-2
点评:本小题主要考查圆的参数方程及直线与圆的位置关系的判断,以及转化与化归的思想方法.本题出现最多的问题应该是计算上的问题,平时要强化基本功的练习,属于基础题.

练习册系列答案
相关题目
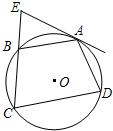 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.