题目内容
给出以下判断:
①若1>
,则a>1; ②若0<α<π,0<β<
,则α-β∈(0,
); ③若|a|>|b|,则a2>b2;
④若a>b,则
<
; ⑤若ac2>bc2,则a>b; ⑥若a>b,c>d,则
>
.
其中正确的有( )个.
①若1>
| 1 |
| a |
| π |
| 2 |
| π |
| 2 |
④若a>b,则
| 1 |
| a |
| 1 |
| b |
| a |
| d |
| b |
| c |
其中正确的有( )个.
分析:解不等式1>
,求出a的取值范围,可判断①的真假;由已知求出-β的范围,进而根据不等式同号可加性,可判断②的真假;根据同号可方性,可判断③的真假;令a>0>b,可根据不等式的基本性质,判断④的真假;根据已知可得c2>0,进而根据不等式的基本性质,判断⑤的真假;令a>b>0,c>0>d,根据不等式的基本性质,判断⑥的真假;
| 1 |
| a |
解答:解:若1>
,则a>1或a<0,故①错误;
若0<α<π,0<β<
,则-
<-β<0,则α-β∈(-
,
),故②错误;
若|a|>|b|,则a2>b2,故③正确;
若a>0>b,则
>
,故④错误
若ac2>bc2,则c2>0,则a>b,故⑤正确;
若a>b>0,c>0>d,则
<
,故⑥错误
故选D
| 1 |
| a |
若0<α<π,0<β<
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
若|a|>|b|,则a2>b2,故③正确;
若a>0>b,则
| 1 |
| a |
| 1 |
| b |
若ac2>bc2,则c2>0,则a>b,故⑤正确;
若a>b>0,c>0>d,则
| a |
| d |
| b |
| c |
故选D
点评:本题又命题的真假判断为载体考查了不等式的基本性质,熟练掌握不等式的基本性质是解答的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
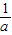 ,则a>1; ②若0<α<π,0<β<
,则a>1; ②若0<α<π,0<β<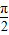 ,则α-β∈(0,
,则α-β∈(0,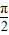 ); ③若|a|>|b|,则a2>b2;
); ③若|a|>|b|,则a2>b2;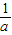 <
<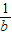 ; ⑤若ac2>bc2,则a>b; ⑥若a>b,c>d,则
; ⑤若ac2>bc2,则a>b; ⑥若a>b,c>d,则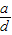 >
>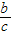 .
.