Question

【题目】已知函数，在原点处切线的斜率为，数列满足为常数且，．

（1）求的解析式；

（2）计算，并由此猜想出数列的通项公式；

（3）用数学归纳法证明你的猜想．

Answer 1

【答案】（1）；（2） ；（3）证明见解析．

【解析】试题分析：（1）求出的导函数，由函数在原点处切线的斜率为可得，可求得的值，从而可得的解析式；（2）由函数解析式，可得递推关系，根据递推关系可依次求出的值，观察前四项共同规律可猜测出数列的通项公式；（3）先验证 时猜想成立，再假设 时猜想成立，只需证明 时，猜想也成立即可.

试题解析：（1）由已知得，，.

（2），则，

，，

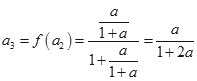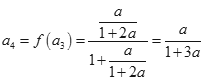由此猜想数列的通项公式应为．

（3）①当时，猜想显然成立，

②假设时，猜想成立，即，

则当时，，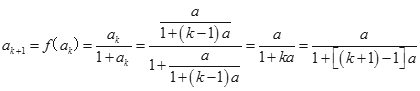

即当时，猜想成立．由①②知，对一切正整数都成立．