题目内容
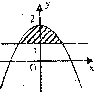
直线y=1与曲线y=-x2+2所围成图形的面积为______.
先求出y=1与曲线y=-x2+2的交点横坐标,得到积分下限为-1,积分上限为1,
直线y=1与曲线y=-x2+2围图形的面积S=∫-11(2-x2)dx=(2x-
x3)|-11=
∴直线y=1与曲线y=-x2+2所围成图形的面积为
故答案为:
.
直线y=1与曲线y=-x2+2围图形的面积S=∫-11(2-x2)dx=(2x-
| 1 |
| 3 |
| 10 |
| 3 |
∴直线y=1与曲线y=-x2+2所围成图形的面积为
| 10 |
| 3 |
故答案为:
| 10 |
| 3 |

练习册系列答案
相关题目