题目内容
如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过P点作⊙O的切线，切点为C，连接AC，若PC=
，∠CPA=________．
30°
分析：在圆中线段利用由切线定理求得∠OCP=Rt∠，进而利用直角三角形PCO中的线段，结合解直角三角形求得∠CPA即可．
解答：
解：连接OC，
PC是⊙O的切线，
∴∠OCP=90°
∵PC=，OC=
AB=3，
∴tan∠CPA=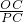
=
=
，
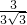∴∠CPA=30°．
故答案为：30°．
点评：此题考查的是直角三角形的性质、与圆有关的比例线段以及切线定理，属于基础题．
分析：在圆中线段利用由切线定理求得∠OCP=Rt∠，进而利用直角三角形PCO中的线段，结合解直角三角形求得∠CPA即可．
解答：
解：连接OC，PC是⊙O的切线，
∴∠OCP=90°
∵PC=
，OC=AB=3，∴tan∠CPA=
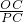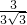==，∴∠CPA=30°．
故答案为：30°．
点评：此题考查的是直角三角形的性质、与圆有关的比例线段以及切线定理，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
21、如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．求证：△PDF∽△POC．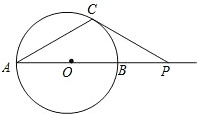
如图，⊙O的直径AB=6cm，P是AB延长线上的一点，过p点作⊙O的切线，切点为C，连接AC，若∠CPA=30°，PC=
如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，DE交AB于点F．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）