题目内容
设等差数列{an}满足a3=5，a10=-9。
（1）求{an}的通项公式；
（2）求{an}的前n项和Sn及使得Sn最大的序号n的值。
（1）求{an}的通项公式；
（2）求{an}的前n项和Sn及使得Sn最大的序号n的值。
解：（1）由an = a1 +（n-1）d及a3=5，a10=-9得
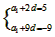解得
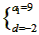
数列{an}的通项公式为an=11-2n；
(2)由(1) 知Sn=na1+d=10n-n2，
因为Sn=-(n-5)2+25.所以n=5时，Sn取得最大值。
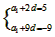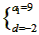
解得数列{an}的通项公式为an=11-2n；
(2)由(1) 知Sn=na1+d=10n-n2，
因为Sn=-(n-5)2+25.所以n=5时，Sn取得最大值。
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
设等差数列{an}满足a5=11，a12=-3，{an}的前n项和Sn的最大值为M，则lgM=（ ）
| A、4 | B、3 | C、2 | D、1 |