题目内容
14.函数f(x)=(x-$\frac{1}{x}$)sinx(-π≤x<0或0<x≤π)的图象大致为( )| A. |  | B. |  | C. |  | D. | 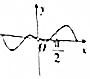 |
分析 判断f(x)的奇偶性,零点个数,计算f($\frac{π}{2}$),即可得出答案.
解答 解:∵f(-x)=(-x+$\frac{1}{x}$)sin(-x)=(x-$\frac{1}{x}$)sinx=f(x),
∴f(x)是偶函数,即f(x)的图象关于y轴对称,
排除D,
令f(x)=0得x-$\frac{1}{x}$=0或sinx=0,
∵-π≤x<0或0<x≤π,
∴x=1或x=-1或x=-π或x=π.
∴f(x)有4个零点,排除A,
又f($\frac{π}{2}$)=$\frac{π}{2}$-$\frac{2}{π}$>0,排除C,
故选B.
点评 本题考查了函数图象的判断,主要从奇偶性、单调性、零点、函数值等各方面判断,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:

(Ⅰ)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.

| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 45 | 75 | 90 | 60 | 30 |
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
5.函数f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期为π,其图象关于直线x=$\frac{π}{3}$对称,则|φ|的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{5π}{6}$ | D. | $\frac{5π}{12}$ |
2.已知命题p:若a>|b|,则a2>b2;命题q:若x2=4,则x=2,.下列说法正确的是( )
| A. | “p∨q”为假命题 | B. | “p∧q”为假命题 | C. | “¬p”为真命题 | D. | “¬q”为假命题 |
3.已知集合A={x|-1≤x<3},B={x∈Z|x2<4},则A∩B=( )
| A. | {0,1} | B. | {-1,0,1,2} | C. | {-1,0,1} | D. | {-2,-1,0,1,2} |