题目内容
已知f(x)=a1x+a2x2+a3x3+…+anxn(n∈N*),且a1,a2,a3,…,an构成一个数列,又f(1)=n2,(1)求数列{an}的通项公式;
(2)求证:f(![]() )<1.
)<1.
答案: (1)解:∵f(1)=a1+a2+a3+…+an(n∈N*),
∴Sn=a1+a2+a3+…+an=n2.
∴a1=S1=1,an=Sn-Sn-1=n2-(n-1)2=2n-1(n≥2).
∴an=2n-1.
(2)证明:∵f(![]() )=1·
)=1·![]() +3·(
+3·(![]() )2+5·(
)2+5·(![]() )3+…+(2n-3)(
)3+…+(2n-3)(![]() )n-1+(2n-1)(
)n-1+(2n-1)(![]() )n,
)n,
∴![]() ·f(
·f(![]() )=1·(
)=1·(![]() )2+3·(
)2+3·(![]() )3+5·(
)3+5·(![]() )4+…+(2n-3)(
)4+…+(2n-3)(![]() )n+(2n-1)(
)n+(2n-1)(![]() )n+1.
)n+1.
两式相减,得![]() ·f(
·f(![]() )=
)=![]() +2·[(
+2·[(![]() )2+(
)2+(![]() )3+(
)3+(![]() )4+…+(
)4+…+(![]() )n]-(2n-1)(
)n]-(2n-1)(![]() )n+1.
)n+1.
∴![]() ·f(
·f(![]() )=
)=![]() +2·
+2·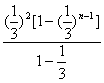 .
.
∴![]() ·f(
·f(![]() )=
)=![]() +
+![]() -(
-(![]() )n-(2n-1)(
)n-(2n-1)(![]() )n+1.
)n+1.
∴f(![]() )=1-
)=1-![]() <1.
<1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.
,Tn为数列{cn}的前n项和,若Tn<λ(bn+1+1),对一切n∈N*都成立,试求λ的取值范围.