题目内容
已知f(x)=a1x+a2x2+…+anxn,且a1,a2,…,an组成等差数列(n为正偶数).又f(1)=n2,f(-1)=n.(1)求数列{an}的通项公式;
(2)证明
＜f(
)＜3(n＞2).
(1)解:设数列{an}的公差为d,∵f(1)=n2,则a1+a2+a3+…+an-1+an=n2.由等差数列的前n项和公式可知
na1+=a1+a2+…+an,
∴a1n+
=n2.①
又∵f(-1)=n,则-a1+a2-a3+a4-a5+…-an-1+an=n(这里运用了n为正偶数),
∴
d=n.②
解得d=2,代入①得
a1n+
·2=n2,
∴a1+n-1=n.∴a1=1.
∴an=1+(n-1)·2=2n-1.
(2)证明:∵f(
)=
+3·(
)2+5·(
)3+…+(2n-1)·(
)n,③
③式两边同乘
得
f(
)=1·(
)2+3·(
)3+…+(2n-3)·(
)n+(2n-1)·(
)n+1,④
③-④得f(
)-
·f(
)=
+2·(
)2+2·(
)3+2·(
)4+…+2·(
)n-(2n-1)·(
)n+1= 
+2［(
)2+(
)3+(
)4+…+(
)n］-(2n-1)·(
)n+1=
+2×
-(2n-1)·(
)n+1=
+1-(
)n-1-(2n-1)·(
)n+1,
∴
f(
)=
-
-
.
∴f(
)=3-
=3-
.
∵
＞0,∴3-
＜3.∴f(
)＜3.
下面证f(
)＞
.令g(n)=f(
)=3-
.
∵n＞2,∴g(2)=3-
=3-
=
,g(3)=3-
=3-
=
,g(4)=3-
.而
＜
＜
,由此可以猜想g(n)是关于n的单调递增函数(数列),证明如下:(注意n是偶数)
∵g(n+2)-g(n)=3-
-(3-
)=
-
＞0,
∴g(2)＜g(4)＜…＜g(n).
∴n＞2且为正偶数时,g(n)是单调递增函数.
∴g(n)＞g(2)=
(n＞2,n为正偶数).
综上所述, 
＜f(
)＜3.故命题成立.
练习册系列答案
相关题目
)与3的大小
,cn=
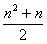,Tn为数列{cn}的前n项和，若Tn＜λ(bn+1+1)，对一切n∈N*都成立，试求λ的取值范围．
)与3的大小.
)+
，g(x)=lnx．
x+m有实数根，求实数m的取值范围；
＜f(
)＜3(n＞2，n∈N*)．