Question

（本小题满分12分）已知函数，，且．

（Ⅰ）若，求的值；

（Ⅱ）当时，求函数的最大值；

Answer 1

（Ⅰ）

（Ⅱ）

【解析】

试题分析：第一问根据函数求导公式和求导法则，可以先求出函数的导函数，之后带入可以求出导函数在某个点处的函数值，第二问把的值带入，之后函数为已知函数，求函数的单调区间，之后求函数的最大值即可.

试题解析：（Ⅰ）函数的定义域为，.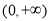

由，解得．

（Ⅱ）由，得．

由，解得；由，解得．

所以函数在区间递增，递减.

因为是在上唯一一个极值点，

故当时，函数取得最大值，最大值为．

考点：求函数的导数，求函数的最值.