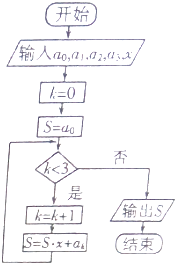
题目内容
【题目】如图,在平面直角坐标系xoy中,F为椭圆E:![]() 的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D.
的右焦点,过F作两条相互垂直的直线AB,CD,与椭圆E分别交于A,B和点C,D.
(1)当AB=![]() 时,求直线AB的方程;
时,求直线AB的方程;
(2)直线AB交直线x=3于点M,OM与CD交于P,CO与椭圆E交于Q,求证:OM∥DQ.

【答案】(1) ![]() (2)见证明
(2)见证明
【解析】
(1)由题意可设直线AB方程y=k(x-2),则直线CD的方程为![]() ,分别与椭圆方程联立,利用弦长公式可得出|AB|,|CD|,根据AB=
,分别与椭圆方程联立,利用弦长公式可得出|AB|,|CD|,根据AB=![]() 解得k,即可得直线AB方程.(2)将直线AB与直线x=3联立,解得M,可得直线OM方程,将直线OM与直线CD联立,解得P点坐标,将直线CD与椭圆联立,利用根与系数的关系、中点坐标公式可得线段CD的中点坐标,得到与点P重合.又点O是CQ的中点,由三角形中位线即可证明结论.
解得k,即可得直线AB方程.(2)将直线AB与直线x=3联立,解得M,可得直线OM方程,将直线OM与直线CD联立,解得P点坐标,将直线CD与椭圆联立,利用根与系数的关系、中点坐标公式可得线段CD的中点坐标,得到与点P重合.又点O是CQ的中点,由三角形中位线即可证明结论.
(1)由题意可设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() .则直线
.则直线![]() 的方程为:
的方程为:![]() .
.
联立![]() ,化为:
,化为:![]() ,
,
![]() ,
,![]() ,
,
则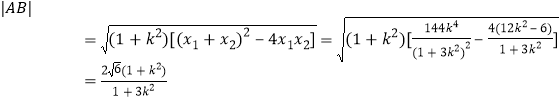 .
.
同理可得: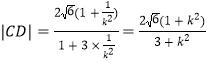 .
.
![]() ,
,![]() .
.
化为:![]() ,解得
,解得![]() .
.
![]() 直线
直线![]() 的方程为:
的方程为:![]() .
.
(2)证明:设直线![]() 的方程为:
的方程为:![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]()
联立![]() ,解得
,解得![]() .
.
可得直线![]() 的方程:
的方程:![]() ,
,
联立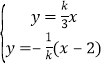 ,解得
,解得![]() .
.
联立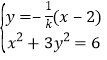 ,化为:
,化为:![]() ,
,
![]() ,可得线段
,可得线段![]() 的中点坐标
的中点坐标![]() ,与点
,与点![]() 重合.
重合.
又点![]() 是
是![]() 的中点,
的中点,![]() ,即
,即![]() .
.

练习册系列答案
相关题目