Question

实系数方程f(x)=x²+ax+2b=0的一个根在(0,1)内，另一个根在(1,2)内，求：

(1)的值域；

(2)(a-1)²+(b-2)²的值域；

(3)a+b-3的值域.

Answer 1

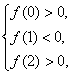解：由题意即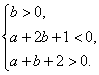

    易求A(-1,0)、B(-2,0).

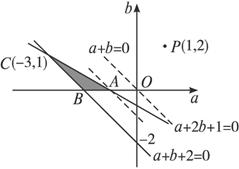
    由∴C(-3,1).

    (1)记P(1,2),k_PC＜＜k_PA,即∈(,1).

    (2)|PC|²=(1+3)²+(2-1)²=17,|PA|²=(1+1)²+(2-0)²=8,|PB|²=(1+2)²+(2-0)²=13.

    ∴(a-1)²+(b-2)²的值域为(8,17).

    (3)令u=a+b-3,即a+b=u+3.

    -2＜u+3＜-1,即-5＜u＜-4.

    ∴a+b-3的值域为(-5,-4).