Question

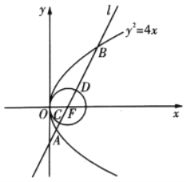
【题目】如图，直线l过抛物线的焦点F且交抛物线于A，B两点，直线l与圆交于C，D两点，若，设直线l的斜率为k，则________.

Answer 1

【答案】

【解析】

由题意设直线的方程与抛物线联立求出两根之和，进而求出弦长的值，再由圆的方程可得圆心为抛物线的焦点可得为圆的直径，求出的值，再由题意可得的值，由题意可得A的横坐标，代入直线的方程，可得A的纵坐标，代入抛物线的方程中可得斜率的平方的值.

由题意圆的圆心为抛物线的焦点F，

再由题意可得直线的斜率不为0，设直线的方程为：，，

设，，联立直线与抛物线的方程：，

整理可得，，所以，

由抛物线的性质可得：弦长，

由题意可得为的直径2，

所以，

而，所以可得：，

因为，

所以，代入直线中可得，

即，

将A点坐标代入抛物线的方程，整理可得，

解得，

因为，所以，

故答案为：.