题目内容
我们把离心率为黄金比 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设 (a>b>0)为“优美椭圆”,F.A分别是它的左焦点和右顶点,B是它短轴的一个端点,则∠ABF等于
(a>b>0)为“优美椭圆”,F.A分别是它的左焦点和右顶点,B是它短轴的一个端点,则∠ABF等于
- A.60°
- B.75°
- C.90°
- D.120°
C
分析:由 可得
可得 验证|FA|2=|FB|2+|AB|2成立所以所以∠FBA等于 90°.
验证|FA|2=|FB|2+|AB|2成立所以所以∠FBA等于 90°.
解答:∵ ,∴
,∴
在三角形FAB中有b2+c2=a2,|FA|=a+c,|FB|=a,|AB|= ,∴|FA|2=(a+c)2=a2+c2+2ac,|FB|2+|AB|2=2a2+b2=3a2-c2,∴|FA|2=|FB|2+|AB|2=
,∴|FA|2=(a+c)2=a2+c2+2ac,|FB|2+|AB|2=2a2+b2=3a2-c2,∴|FA|2=|FB|2+|AB|2= ,所以∠FBA等于 90°.
,所以∠FBA等于 90°.
故选C.
点评:解决此类问题关键是熟练掌握椭圆的几何性质,以及利用边长关系判断三角形的形状的问题.
分析:由
 可得
可得 验证|FA|2=|FB|2+|AB|2成立所以所以∠FBA等于 90°.
验证|FA|2=|FB|2+|AB|2成立所以所以∠FBA等于 90°.解答:∵
 ,∴
,∴
在三角形FAB中有b2+c2=a2,|FA|=a+c,|FB|=a,|AB|=
 ,∴|FA|2=(a+c)2=a2+c2+2ac,|FB|2+|AB|2=2a2+b2=3a2-c2,∴|FA|2=|FB|2+|AB|2=
,∴|FA|2=(a+c)2=a2+c2+2ac,|FB|2+|AB|2=2a2+b2=3a2-c2,∴|FA|2=|FB|2+|AB|2= ,所以∠FBA等于 90°.
,所以∠FBA等于 90°.故选C.
点评:解决此类问题关键是熟练掌握椭圆的几何性质,以及利用边长关系判断三角形的形状的问题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
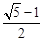 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设
 为“优美椭圆”,F、A分别是左焦点和右顶点,B是短轴的一个端点,则
为“优美椭圆”,F、A分别是左焦点和右顶点,B是短轴的一个端点,则 (
)
(
) 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设 (a>b>0)
(a>b>0) 的椭圆称为“优美椭圆”.设
的椭圆称为“优美椭圆”.设 (a>b>0)为“优美椭圆”,F.A分别是它的左焦点和右顶点,B是它短轴的一个端点,则∠ABF等于( )
(a>b>0)为“优美椭圆”,F.A分别是它的左焦点和右顶点,B是它短轴的一个端点,则∠ABF等于( )