题目内容
在如图的几何体中,四边形 为正方形,四边形
为正方形,四边形 为等腰梯形,
为等腰梯形, ∥
∥ ,
, ,
, ,
, .
.
(1)求证: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)证明见解析;(2) .
.
解析试题分析:(1)要证线面垂直,就是要证直线与平面内的两条相交直线垂直,在题中已经有 ,另一条直线应该是
,另一条直线应该是 ,在
,在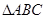 中,由已知易证;(2)求直线
中,由已知易证;(2)求直线 与平面
与平面 所成的角,要找到
所成的角,要找到 在平面
在平面 内的射影,这里线面的交点没给出,垂直关系也比较难找,但由(1)的证明可得
内的射影,这里线面的交点没给出,垂直关系也比较难找,但由(1)的证明可得 两两垂直,因此我们可以以他们为坐标轴建立空间直角坐标系,用空间向量来求线面角,只要求出平面
两两垂直,因此我们可以以他们为坐标轴建立空间直角坐标系,用空间向量来求线面角,只要求出平面 的一个法向量
的一个法向量 ,那么向量
,那么向量 与
与 的夹角的余弦值等于直线
的夹角的余弦值等于直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)证明:因为 ,
,
在△ 中,由余弦定理可得
中,由余弦定理可得 .所以
.所以 .所以
.所以 .
.
因为 ,
, ,
, 、
、 平面
平面 ,所以
,所以 平面
平面 . -4分
. -4分
(2)由(1)知, 平面
平面 ,
, 平面
平面 ,所以
,所以 .
.
因为平面 为正方形,所以
为正方形,所以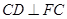 .
.
因为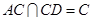 ,所以
,所以 平面
平面 .
.
所以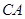 ,
, ,
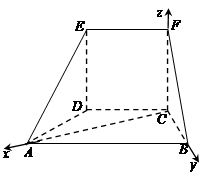
, 两两互相垂直,建立如图的空间直角坐标系
两两互相垂直,建立如图的空间直角坐标系 .
.
因为 是等腰梯形,且
是等腰梯形,且 ,
,
所以 .
.
不妨设 ,则
,则 ,
, ,
, ,
, ,
, ,
,





考点:(1)线面垂直;(2)直线与平面所成的角.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
 的底面边长为8的正方形,四条侧棱长均为
的底面边长为8的正方形,四条侧棱长均为 .点
.点 分别是棱
分别是棱 上共面的四点,平面
上共面的四点,平面 平面
平面 ,
, 平面
平面 .
.
 ,求四边形
,求四边形
 是边长为2的正方形,
是边长为2的正方形, 平面
平面 ,
, ,且
,且 .
.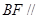 平面
平面 ;
; 平面
平面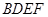 ;
; 的体积。
的体积。
 底面ABCD,侧棱
底面ABCD,侧棱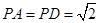 ,底面ABCD为直角梯形,其中BC//AD,AB
,底面ABCD为直角梯形,其中BC//AD,AB

 中,
中, ,G是
,G是 上的动点。
上的动点。
 ;
; 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;
 中,
中, ,
,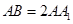 ,
, 是
是 的中点,△
的中点,△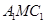 是等腰三角形,
是等腰三角形, 为
为 的中点,
的中点, 为
为 上一点.
上一点.
 ∥平面
∥平面 ;
; 中,
中, 平面
平面 ,底面
,底面 .
.
 平面
平面 ;
; 平面
平面 ;
; 是
是 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.