题目内容

给出如下命题：
①y=x⁰与y=1不是同一函数；　　　
②函数y=a^x+1+1（a＞1）的图象过定点（-1，2）；
③ $数学公式$ 是其定义域上的单调减函数；　
④ $数学公式$ 与y=-log₂x的图象关于y=x对称．
其中正确命题的序号是________．（请填上你认为所有正确命题的序号）

②④
分析：①y=x⁰定义域为（-∞，0）∪（0，+∞），y=1定义域为R；
②函数y=a^x+1+1（a＞1）的图象过定点（-1，2）；
③ $\text{[math]}$ 在（-∞，0）是单调减函数，在（0，+∞）上是单调减函数；
④ $\text{[math]}$ 与y=-log₂x互为反函数．
解答：①y=x⁰定义域为（-∞，0）∪（0，+∞），y=1定义域为R，故不是同一函数；
②函数y=a^x+1+1（a＞1）的图象过定点（-1，2），为真命题；
③ $\text{[math]}$ 在（-∞，0）是单调减函数，在（0，+∞）上是单调减函数，故命题不正确；
④由 $\text{[math]}$ 求得 $\text{[math]}$ ，再将x与y互换可得y=-log₂x，所以 $\text{[math]}$ 与y=-log₂x的图象关于y=x对称，故正确．
所以正确的命题是②④
故答案为：②④
点评：本题考查函数的概念，考查函数的单调性，考查反函数的概念，解题的关键是逐一判断，属于中档题．

练习册系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

课内外古诗文阅读特训系列答案

课内外文言文系列答案

古诗文高效导学系列答案

古诗文夯基与积累系列答案

相关题目

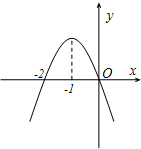已知函数y=f（x）的导函数y=f'（x）的图象如图所示，给出如下命题：
①0是函数y=f（x）的一个极值点；
②函数y=f（x）在x=-

处切线的斜率小于零；
③f（-1）＜f（0）；
④当-2＜x＜0时，f（x）＞0．
其中正确的命题是

．（写出所有正确命题的序号）

已知函数y=f（x）在R上是偶函数，对任意x∈R都有f（x+6）=f（x）+f（3），当x₁，x₂∈[0，3]且x₁≠x₂时，

＞0，给出如下命题：
①函数y=f（x）在[-9，6]上为增函数
②直线x=-6是y=f（x）图象的一条对称轴
③f（3）=0
④函数y=f（x）在[-9，9]上有四个零点．
其中所有正确命题的序号为

（2013•泸州一模）设集合s为非空实数集，若数η（ξ）满足：
（1）对?x∈S，有x≤η（x≥ξ），即η（ξ）是S的上界（下界）；
（2）对?a＜η（a＞ξ），?x_o∈S，使得x_o＞a（x_o＜a），即η（ξ）是S的最小（最大）上界（下界），则称数η（ξ）为数集S的上（下）确界，记作η=supS（ξ=infS）．
给出如下命题：
①若 S={x|x²＜2}，则 supS=-

；
②若S={x|x=n|，x∈N}，则infS=l；
③若A、B皆为非空有界数集，定义数集A+B={z|z=x+y，x∈A，y∈B}，则sup（A+B）=supA+supB．
其中正确的命题的序号为

（填上所有正确命题的序号）．

给出如下命题：
①y=x⁰与y=1不是同一函数；
②函数y=a^x+1+1（a＞1）的图象过定点（-1，2）；
③y=

是其定义域上的单调减函数；
④y=(

)x与y=-log₂x的图象关于y=x对称．
其中正确命题的序号是

．（请填上你认为所有正确命题的序号）