Question

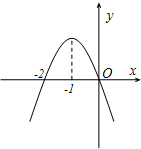已知函数y=f（x）的导函数y=f'（x）的图象如图所示，给出如下命题：
①0是函数y=f（x）的一个极值点；
②函数y=f（x）在x=-

1

2

处切线的斜率小于零；
③f（-1）＜f（0）；
④当-2＜x＜0时，f（x）＞0．
其中正确的命题是

 

．（写出所有正确命题的序号）

Answer 1

分析：x＞0时，f'（x）＜0；x=0时，f'（x）=0；x＜0时，f'（x）＞0．所以0是函数y=f（x）的一个极值点．由f'（-

1

2

）＞0，知函数y=f（x）在x=-

1

2

处切线的斜率大于0．由-2＜x＜0时，f'（x）＞0，知f（-1）＜f（0）．

解答：解：∵x＞0时，f'（x）＜0；x=0时，f'（x）=0；x＜0时，f'（x）＞0．
∴0是函数y=f（x）的一个极值点．
∵f'（-

1

2

）＞0，∴函数y=f（x）在x=-

1

2

处切线的斜率大于0．
∵-2＜x＜0时，f'（x）＞0，∴f（-1）＜f（0）．
-2＜x＜0时，f'（x）＞0．
故答案为：①③．

点评：本题考查命题的真假判断和应用，解题时要熟练掌握导函数的图象和性质．