题目内容
(12分)已知函数 是定义在
是定义在 上的偶函数,已知当
上的偶函数,已知当 时,
时, .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间;
的单调递增区间;
(3)求 在区间
在区间 上的值域。
上的值域。
【答案】
(1)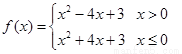
(2)函数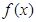 的单调递增区间为
的单调递增区间为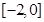 和
和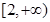
(3)值域为(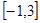
【解析】
试题分析:解:(1)∵函数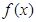 是定义在
是定义在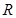 上的偶函数
上的偶函数
∴对任意的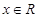 都有
都有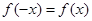 成立
成立
∴当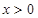 时,
时, 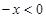 即
即
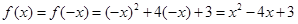
∴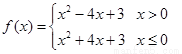 4分
4分
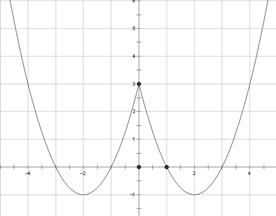
(2)图形如图所示,函数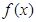 的单调递增区间为
的单调递增区间为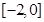 和
和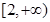 .(写成开区间也可以)8分
.(写成开区间也可以)8分
(3)值域为(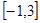 12分
12分
考点:函数的单调性和解析式的运用
点评:解决该试题的关键是利用二次函数的性质,以及奇偶性来分析得到函数的解析式,并求解单调性,属于基础题。

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若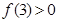 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;