题目内容
是否存在常数 ,使等式
,使等式 对于一切
对于一切 都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
都成立?若不存在,说明理由;若存在,请用数学归纳法证明?
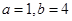 ,证明详见解析.
,证明详见解析.
解析试题分析:先从特殊情形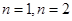 ,等式必须成立,求出
,等式必须成立,求出 值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
值,然后用数学归纳法加以证明,在这里必须指出的是:若题目没有讲要用数学归纳法证明,我们也应从数学归纳法考虑,因为等式的左边我们无法通过数列求和的知识解决,其次本题是与自然数有关的命题证明,我们应优先考虑数学归纳法,证明时必须严格遵循数学归纳法的证题步骤,做到规范化.
试题解析:若存在常数 使等式成立,则将
使等式成立,则将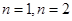 代入上式,有
代入上式,有 得
得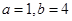 ,即有
,即有 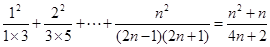 对于一切
对于一切 成立. 5分
成立. 5分
数学归纳法证明如下:
证明如下:(1)当 时,左边=
时,左边=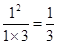 ,右边=
,右边= ,所以等式成立,
,所以等式成立,
(2)假设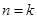 (
( 且
且 )时等式成立,即
)时等式成立,即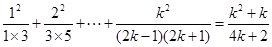 ,
,
当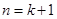 时,
时,

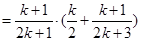
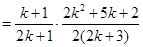


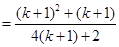
也就是说,当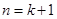 时,等式成立,
时,等式成立,
综上所述,可知等式对任何 都成立. 12分
都成立. 12分
考点:数学归纳法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前 项和为
项和为 ,且满足
,且满足
 .
. ,
, ,
, ,
, 的值并写出其通项公式;
的值并写出其通项公式;
 +
+ +
+ +…+
+…+ 的值.
的值. 都是正实数,且
都是正实数,且 .求证:
.求证: 与
与 中至少有一个成立.
中至少有一个成立. 满足a1=0且
满足a1=0且 -
- = 1.
= 1. ,记Sn=
,记Sn= ,证明:Sn<1.
,证明:Sn<1. 是线段
是线段 上一点,则
上一点,则 ;将它类比到平面的情形是:若
;将它类比到平面的情形是:若 内一点,有
内一点,有 ;将它类比到空间的情形应该是:若
;将它类比到空间的情形应该是:若 内一点,则有__________________________.
内一点,则有__________________________. 的性质
的性质 =
= 类比得到复数
类比得到复数 的性质
的性质 ;
;