题目内容
在某种工业品的生产过程中,每日次品数y是每日产量x的函数：y=
该工厂售出一件正品可获利A元,但生产一件次品就损失
元,为了获得最大利润,日产量应为多少?
思路分析：最大利润等于正品获利减去次品损失，根据已知条件列出利润关于日产量的函数关系式，利用导数求出最值.
解：在每天生产的x件产品中,x-y(x)是正品数,y是次品数,每日获利总数为T(x)=A(x-y)-Ay,要使T(x)取最大值,则T′(x)=A(1-y′).令T′(x)=0,得y′=
,因为已假定y=
易知当x＞100时,每一件产品都是次品,公司就要赔钱,最佳日产量只能在x≤100时求得.由y′=
x=89.4,但产品个数必须是自然数,因此产品个数应是89或90件.又由于T(89)=79.11A,T(90)=79.09A,所以每日生产89件将获得最大利润.
练习册系列答案
相关题目
该工厂售出一件正品可获利A元，但生产一件次品就损失
元，为了获得最大利润，日产量应定为多少？
元，
与每日产量
的函数关系式为
，该工厂售出一件正品可获利
元，但生产一件次品就损失
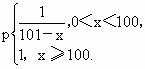
元，为了获得最大利润，日产量应定为多少？