题目内容
在某产品的制造过程中,次品率p依赖于日产量x,已知
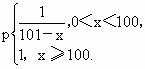
其中x为正整数.又该厂每生产出一件正品可盈利A元,但每产出一件次品就要损失 元,
元,
(1)将该厂的日盈利额T(元)表示为日产量x(个)的函数,并指出这个函数的定义域;
(2)为了获得最大盈利,该厂的日产量应定为多少?
答案:略
解析:
解析:
|
解: (1)设日产量为x个,则次品为xp个,正品x(1-p)个.于是日盈利额  . .
∵ x≥100时,p=1,产品全部是次品,工厂不盈利,不合题意,∴  .故所求函数为 .故所求函数为 ,函数的定义域为{x|0<x<100,xÎ
N}. ,函数的定义域为{x|0<x<100,xÎ
N}.
(2) 将函数关系式变形为 . .
设 101-x=t, , ,
因为 0<x<100,所以1<t<101.用单调性定义不难验证  在 在 上是减函数,在 上是减函数,在 上是增函数,又∵ 上是增函数,又∵ ,而tÎ
N, ,而tÎ
N,
∴ f(t)在(0,11)上递减,在[12,+∞)上递增.而 , ,
故为获得最大盈利,该厂的日产量应定为 89个. |

练习册系列答案
相关题目