题目内容
设f(x)=x2-4x+m, 在区间D=[1,3]上,满足:对于任意的a∈D,存在实数x0∈D,使得f(x0)≤f(a),g(x0)≤g(a)且g(x0)=f(x0);那么在D=[1,3]上f(x)的最大值是
在区间D=[1,3]上,满足:对于任意的a∈D,存在实数x0∈D,使得f(x0)≤f(a),g(x0)≤g(a)且g(x0)=f(x0);那么在D=[1,3]上f(x)的最大值是
- A.5
- B.
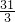
- C.

- D.4
A
分析:先确定 在区间D=[1,3]上的最大值为5,再根据定义,即可求得结论.
在区间D=[1,3]上的最大值为5,再根据定义,即可求得结论.
解答:∵ 在区间[1,2]上单调递减,在[2,3]上单调递增,g(1)=5,g(3)=
在区间[1,2]上单调递减,在[2,3]上单调递增,g(1)=5,g(3)=
∴ 在区间D=[1,3]上的最大值为5
在区间D=[1,3]上的最大值为5
∵对于任意的a∈D,存在实数x0∈D,使得f(x0)≤f(a),g(x0)≤g(a)且g(x0)=f(x0)
∴在D=[1,3]上f(x)的最大值即为 在区间D=[1,3]上的最大值
在区间D=[1,3]上的最大值
∴在D=[1,3]上f(x)的最大值为5
故选A.
点评:本题考查函数的最值,考查学生分析解决问题的能力,属于中档题.
分析:先确定
 在区间D=[1,3]上的最大值为5,再根据定义,即可求得结论.
在区间D=[1,3]上的最大值为5,再根据定义,即可求得结论.解答:∵
 在区间[1,2]上单调递减,在[2,3]上单调递增,g(1)=5,g(3)=
在区间[1,2]上单调递减,在[2,3]上单调递增,g(1)=5,g(3)=
∴
 在区间D=[1,3]上的最大值为5
在区间D=[1,3]上的最大值为5∵对于任意的a∈D,存在实数x0∈D,使得f(x0)≤f(a),g(x0)≤g(a)且g(x0)=f(x0)
∴在D=[1,3]上f(x)的最大值即为
 在区间D=[1,3]上的最大值
在区间D=[1,3]上的最大值∴在D=[1,3]上f(x)的最大值为5
故选A.
点评:本题考查函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目