题目内容
(本小题满分13分)如图,在四棱锥 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, , 点
, 点 是
是 的中点,
的中点, ,且交
,且交 于点
于点 .
.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:直线 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
(Ⅰ)(Ⅱ)详见解析;(Ⅲ)
【解析】
试题分析:法一:用几何关系证明和求值.(Ⅰ)连结 交
交 于
于 ,证
,证 即可;(Ⅱ)先证
即可;(Ⅱ)先证 平面
平面 ,再证
,再证 平面
平面 即可;(Ⅲ)由三垂线定理先作出二面角
即可;(Ⅲ)由三垂线定理先作出二面角 的平面角
的平面角 ,根据数据关系求之即可.
,根据数据关系求之即可.
法二:建立空间直角坐标系,用空间向量证明求解.
试题解析:方法一:(Ⅰ)证明:连结 交
交 于
于 ,连结
,连结 .
.

 是正方形,∴
是正方形,∴  是
是 的中点.
的中点.
 是
是 的中点,∴
的中点,∴ 是△
是△ 的中位线.
的中位线.
∴ . 2分
. 2分
又∵ 平面
平面 ,
,
 平面
平面 ,
,
∴
 平面
平面 . 4分
. 4分
(Ⅱ)证明:由条件有
∴  平面
平面 ,∴
,∴ 6分
6分
又∵  是
是 的中点,∴
的中点,∴
∴ 平面
平面 ∴
∴
由已知 ,∴
,∴ 平面
平面 8分
8分
(Ⅲ)由(Ⅱ)知 面
面 ,则直线
,则直线 在面
在面 内的射影为
内的射影为 ,
,
∴ 为所求的直线
为所求的直线 与面
与面 所成的角. 10分
所成的角. 10分
又 ,∴在
,∴在 中
中 ∴
∴
又
由 可得
可得 ∴
∴ .∴
.∴
12分
∴直线 与平面
与平面 所成角的余弦值为
所成角的余弦值为 . 13分
. 13分
考点:空间直线与平面平行、垂直的性质与判定.

练习册系列答案
相关题目
 的图象是
的图象是
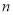 值等于7,则输出的
值等于7,则输出的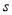 的值为( )
的值为( )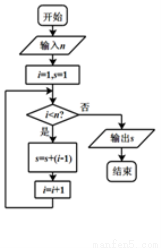
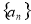 中,前10项的和等于前5项的和.若
中,前10项的和等于前5项的和.若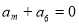 则
则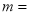 ( )
( )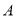 .10
.10 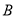 .9
.9 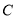 .8
.8 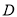 .2
.2 (a>0,b>0)的一条渐近线为
(a>0,b>0)的一条渐近线为 ,则它的离心率为( )
,则它的离心率为( ) B.
B.  C.
C.  D.
D. 

 , 且
, 且 与
与 在直线l的方向向量上的投影的长度相等,则直线l的斜率为
在直线l的方向向量上的投影的长度相等,则直线l的斜率为 B.
B. C.
C. D.
D.
 上的点向圆
上的点向圆 引切线,则切线长的最小值为 .
引切线,则切线长的最小值为 . 中,
中, ,
, ,平面
,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 分别是
分别是 的中点,
的中点, .
.

 ;
; 平面
平面 ;
; ,求几何体
,求几何体 的体积.
的体积.