题目内容
如图,某小区准备在一直角围墙![]() 内的空地上植造一块“绿地
内的空地上植造一块“绿地![]() ”,其中
”,其中![]() 长为定值
长为定值![]() ,
,![]() 长可根据需要进行调节(
长可根据需要进行调节(![]() 足够长).现规划在
足够长).现规划在![]() 的内接正方形
的内接正方形![]() 内种花,其余地方种草,且把种草的面积
内种花,其余地方种草,且把种草的面积![]() 与种花的面积
与种花的面积![]() 的比值
的比值![]() 称为“草花比
称为“草花比![]() ”.
”.
(Ⅰ)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(Ⅱ)当![]() 为多长时,
为多长时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?

⑴![]() ⑵当
⑵当![]() 长为
长为![]() 时,
时,![]() 有最小值1
有最小值1
解析:
由条件知需找到边与角的关系,分析图形建模. (Ⅰ)因为![]() ,所以
,所以![]() 的面积为
的面积为![]() (
(![]() ) 设正方形
) 设正方形![]() 的边长为
的边长为![]() ,则由
,则由![]() ,得
,得![]() ,
,
解得![]() ,则
,则![]()
所以![]() ,则
,则![]() (Ⅱ)因为
(Ⅱ)因为![]() ,所以
,所以![]()
![]() 当且仅当
当且仅当![]() 时取等号,此时
时取等号,此时![]() .所以当
.所以当![]() 长为
长为![]() 时,
时,![]() 有最小值1
有最小值1
三角与函数综合知识建立模型是近两年高考的热点题型之一.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
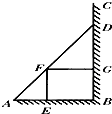 如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值
如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2的比值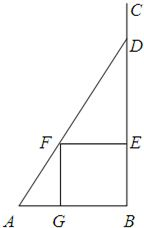 如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2比
如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长).现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积S1与种花的面积S2比 本题共3个小题,第1、2小题满分各5分,第3小题满分6分.
本题共3个小题,第1、2小题满分各5分,第3小题满分6分. 内的空地上植造“绿地
内的空地上植造“绿地 ”,其中
”,其中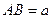 ,
,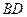 长可根据需要进行调节(
长可根据需要进行调节(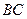 足够长),现规划在
足够长),现规划在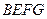 内种花,其余地方种草,设种草的面积
内种花,其余地方种草,设种草的面积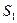 与种花的面积
与种花的面积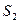 的比
的比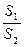 为
为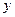 ,
,
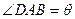 ,将
,将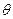 的函数关系;
的函数关系;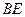 为多长时,
为多长时, ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长)。现规划在
ABD”,其中AB长为定值a,BD长可根据需要进行调节(BC足够长)。现规划在 与种花的面积
与种花的面积 的比值
的比值 称为“草花比y”
称为“草花比y”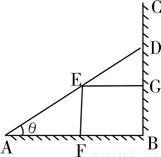
 ,将y表示成
,将y表示成 的函数关系式。
的函数关系式。