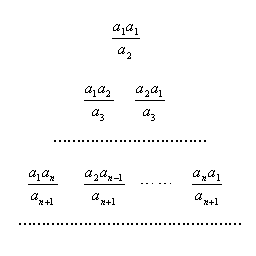
题目内容
已知数列![]() 满足:
满足:![]() ,且
,且![]()
(1)设![]() ,证明数列
,证明数列![]() 是等差数列;
是等差数列;
(2)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,证明
项和,证明![]() .
.
解:(1) 解法一:![]() ,
,![]()
![]()
![]() 为等差数列 4分
为等差数列 4分
解法二:
 ……4分
……4分
(2)由(1)![]() ,从而
,从而![]() 6分
6分
(3)解法一:![]()
![]()
![]() , 6分
, 6分
![]() 当
当![]() 时,
时,![]() ,不等式的左边=7,不等式成立
,不等式的左边=7,不等式成立
当![]() 时,
时, ![]() 故只要证
故只要证![]() ,
,
如下用数学归纳法给予证明:
①当![]() 时,
时,![]() ,
,![]() 时,不等式成立;
时,不等式成立;
![]() ②假设当
②假设当![]() 时,
时,![]() 成立
成立
当![]() 时,
时, ![]()
只需证: ![]() ,即证:
,即证: ![]()
令![]() ,则不等式可化为:
,则不等式可化为:![]()
即![]() 令
令![]() ,则
,则![]()
![]() 在
在![]() 上是减函数又
上是减函数又![]() 在
在![]() 上连续,
上连续, ![]() ,故
,故![]()
当![]() 时,有
时,有![]()
![]() 当
当![]() 时,所证不等式对
时,所证不等式对![]() 的一切自然数均成立综上所述,
的一切自然数均成立综上所述,![]() 成立. 14分
成立. 14分
解法二:同一法可得:![]()
下面证明:![]()
记![]()



练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 满足
满足 ,
, ,且对任意
,且对任意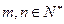 都有
都有
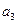 ,
, ;
;
 ,证明:
,证明: 是等差数列;
是等差数列;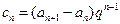
 ,求数列
,求数列 的前n项和
的前n项和 .
. 满足
满足 ,
, ,且
,且 ,
, 。
。 的前
的前 项和
项和 .
. 满足
满足 ,
, ,且
,且
 ;
;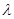 ,使得数列
,使得数列 为等差数列,求
为等差数列,求 满足
满足 ,
, (
( 且
且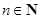 )
) 是常数列;
是常数列; 时,求数列
时,求数列 项和.
项和.