题目内容
已知圆![]()
(1)求证:当![]() 时,直线l与圆C恒有两个不同的交点;
时,直线l与圆C恒有两个不同的交点;
(2)设l与圆交于A、B两点,若![]() 的倾斜角;
的倾斜角;
(3)求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线。
解法一:
(1)直线![]() 而P(1,1)在圆
而P(1,1)在圆![]() 内部(
内部(![]() )
)
故当![]() 时,直线l与该圆恒有两个不同的交点。
时,直线l与该圆恒有两个不同的交点。
(2)如图,作CM⊥AB于M,连CA。

当![]()
而![]()
在Rt△CAM中,![]()
![]()
在Rt△CPM中,
![]()
从而AB的倾斜角为![]() 由圆的对称性知,AB倾斜角还可为
由圆的对称性知,AB倾斜角还可为![]()
(3)M是AB的中点,
![]()
![]() 点轨迹是以线段CP为直径的圆,其方程为
点轨迹是以线段CP为直径的圆,其方程为![]()
解法二:
(1)直线![]() 中,得
中,得
![]() ①
①
![]()
∴直线l与该圆恒有两个不同的交点。
(2)由方程①,可知![]()
![]()
![]()
![]()
![]() ,即AB的倾斜角为
,即AB的倾斜角为![]()
(3)设M的坐标为![]()
![]()

即![]()
轨迹为以![]() 为半径的圆。
为半径的圆。

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆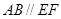 ,矩形
,矩形 和圆
和圆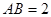 ,
, .
. 平面
平面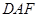 ;
;  所成角的大小;
所成角的大小; 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为 ?
?
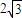 ,AC=BC,F是AB上一点,且
,AC=BC,F是AB上一点,且 ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知 .
.