题目内容
![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆上,
在圆上,![]() ,矩形
,矩形![]() 所在平面与圆
所在平面与圆![]() 所在平面互相垂直,已知
所在平面互相垂直,已知![]()
![]() 。
。
(1)求证:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角;
所成的角;
(3)在![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]()
![]() 平面
平面![]() ?若不存在,请
?若不存在,请![]() 说明理由;若存在,请找出这一点,并证明之。
说明理由;若存在,请找出这一点,并证明之。

(1)证明见解析。
(2)![]()
(3)![]() 是
是![]() 的中点,证明见解析。
的中点,证明见解析。
解析:
(1)证明:因为平面![]()
![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
, ![]()
![]() ;
;
又![]() 为圆
为圆![]() 的直径,
的直径,![]() ,
,
![]() ,
,
![]() 平面
平面![]() ; (5分)
; (5分)

(2)因为平面![]() 与平面
与平面![]() 互相垂直,
互相垂直,
所以交线![]() 是直线
是直线![]() 在平面
在平面![]() 上的射影,
上的射影,
所以![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角.
所成的角.
(7分)
因为![]() 且
且![]() , 所以四边形
, 所以四边形![]() 是平行四边形,
是平行四边形,
又![]() , 所以
, 所以![]() 是菱形,且
是菱形,且![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,
直线![]() 与平面
与平面![]() 所成的角的大小为
所成的角的大小为![]() ; (10分)
; (10分)
(3)![]() 是
是![]() 的中点.
的中点.
证明:连![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
由(2)知,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() . (15分)
. (15分)
(注:用向量方法相应给分.)

练习册系列答案
相关题目
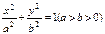 的离心率为
的离心率为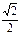 .
.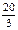 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程;
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆W方程; 的值.
的值.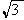 y+8=0上.当∠F1RF2取最大值时,求
y+8=0上.当∠F1RF2取最大值时,求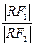 的值.
的值.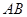 为圆
为圆 的直径,点
的直径,点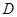 为线段
为线段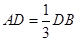 ,点
,点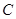 为圆
为圆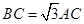 .点
.点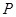 在圆
在圆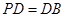 .
.
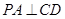 ;
;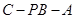 的余弦值.
的余弦值.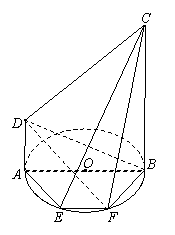 如图,
如图,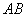 为圆
为圆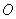 的直径,点
的直径,点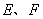 在圆上,
在圆上,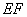 ,
,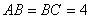 ,
,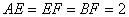 ,
,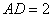 。
。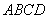 所在平面与圆
所在平面与圆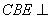 平面
平面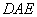 ;
;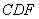 与平面
与平面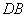 上是否存在一点
上是否存在一点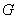 ,使
,使 ∥平面
∥平面 为圆
为圆 的直径,点
的直径,点
 在圆上,
在圆上, ,矩形
,矩形 所在
所在
 .
. 平面
平面 ;
; 与平面
与平面 上是否存在一点
上是否存在一点 ,
,
 平面
平面 ?若不存在,请说明理由;
?若不存在,请说明理由;