题目内容
如图,C、D是以AB为直径的圆上两点,AB=2AD=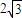 ,AC=BC,F是AB上一点,且
,AC=BC,F是AB上一点,且 ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上,已知 .
.(1)求证:AD⊥平面BCE;
(2)求证:AD∥平面CEF;
(3)求三棱锥A-CFD的体积.

【答案】分析:(1)可先证明AD与两相交直线CE,BD垂直,利用线面垂直的判定定理证明线面垂直
(2)在图形中取BD中点E,连接EF,可得出EF∥AD,再由线面平行的判定定理即可证明AD∥平面CEF;
(3)由题设条件知CE即是此棱锥的高,故求出底面三角形AFD的面积即可,此需要先求出F到AD的距离,易求.
解答:(1)证明:依题意:AD⊥BD
∵CE⊥平面ABD∴CE⊥AD
∵BD∩CE=E,∴AD⊥平面BCE.
(2)证明: Rt△BCE中,
Rt△BCE中, ,
,
∴BE=2(5分)Rt△ABD中, ,
,
∴BD=3.(6分)
∴ .
.
∴AD∥EF∵AD在平面CEF外
∴AD∥平面CEF.
(3)解:由(2)知AD∥EF,AD⊥ED,且ED=BD-BE=1
∴F到AD的距离等于E到AD的距离,为1.
∴ .
.
∵CE⊥平面ABD
∴ .
.
点评:本题考查直线与平面垂直的判定,直线与平面平行的判定,求棱锥的体积,求解本题的关键是创造出线面垂直、线面平行的条件,熟知相关的定理是求解这一类题的保证.代数多做题,几何背定理,道出了学习几何的方法.
(2)在图形中取BD中点E,连接EF,可得出EF∥AD,再由线面平行的判定定理即可证明AD∥平面CEF;
(3)由题设条件知CE即是此棱锥的高,故求出底面三角形AFD的面积即可,此需要先求出F到AD的距离,易求.
解答:(1)证明:依题意:AD⊥BD
∵CE⊥平面ABD∴CE⊥AD
∵BD∩CE=E,∴AD⊥平面BCE.
(2)证明:
 Rt△BCE中,
Rt△BCE中, ,
,
∴BE=2(5分)Rt△ABD中,
 ,
,
∴BD=3.(6分)
∴
 .
.∴AD∥EF∵AD在平面CEF外
∴AD∥平面CEF.
(3)解:由(2)知AD∥EF,AD⊥ED,且ED=BD-BE=1
∴F到AD的距离等于E到AD的距离,为1.
∴
 .
.∵CE⊥平面ABD
∴
 .
.点评:本题考查直线与平面垂直的判定,直线与平面平行的判定,求棱锥的体积,求解本题的关键是创造出线面垂直、线面平行的条件,熟知相关的定理是求解这一类题的保证.代数多做题,几何背定理,道出了学习几何的方法.

练习册系列答案
相关题目
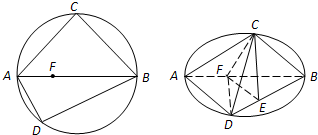 如图,C、D是以AB为直径的圆上两点,AB=2AD=
如图,C、D是以AB为直径的圆上两点,AB=2AD=
 (2013•济宁二模)如图:C、D是以AB为直径的圆上两点,AB=2AD=2
(2013•济宁二模)如图:C、D是以AB为直径的圆上两点,AB=2AD=2 在线段
在线段 上,且
上,且
 ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
 ,AC=BC,F是AB上一点,且AF=
,AC=BC,F是AB上一点,且AF= AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
AB,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.