题目内容
 如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点 E.
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点 E.(1)求证:E为AB的中点;
(2)求线段FB的长.
考点:与圆有关的比例线段,弦切角
专题:选作题,立体几何
分析:(1)根据∠CDO=∠FDO,BC是的切线,且CF是圆D的弦,得到∠BCE=
∠CDF,即∠CDO=∠BCE,得到两个三角形全等,得到线段相等,得到结论.
(2)根据两个角对应相等,得到两个三角形相似,得到对应边成比例,根据所给的长度,代入比例式,得到要求的线段.
| 1 |
| 2 |
(2)根据两个角对应相等,得到两个三角形相似,得到对应边成比例,根据所给的长度,代入比例式,得到要求的线段.
解答:
(1)证明:连接DF,DO,则∠CDO=∠FDO,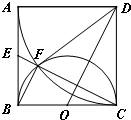
因为BC是的切线,且CF是圆D的弦,
所以∠BCE=
∠CDF,即∠CDO=∠BCE,
故Rt△CDO≌Rt△BCE,
所以EB=OC=
AB.…(5分)
所以E是AB的中点.
(2)解:连接BF,
∵∠BEF=∠CEB,∠ABC=∠EFB
∴△FEB∽△BEC,
得
=
,
∵ABCD是边长为a的正方形,
∴BF=
a.

因为BC是的切线,且CF是圆D的弦,
所以∠BCE=
| 1 |
| 2 |
故Rt△CDO≌Rt△BCE,
所以EB=OC=
| 1 |
| 2 |
所以E是AB的中点.
(2)解:连接BF,
∵∠BEF=∠CEB,∠ABC=∠EFB
∴△FEB∽△BEC,
得
| BF |
| BE |
| CB |
| CE |
∵ABCD是边长为a的正方形,
∴BF=
| ||
| 5 |
点评:本题考查相似三角形的判定和性质,考查圆周角定理,本题解题的关键是得到三角形全等和三角形相似,本题是一个中档题目.

练习册系列答案
相关题目
 已知f(x)=ax3+bx2+cx的导函数y=f′(x)的简图,它与x轴的交点是(0,0)和(1,0),又f′(
已知f(x)=ax3+bx2+cx的导函数y=f′(x)的简图,它与x轴的交点是(0,0)和(1,0),又f′(