题目内容
（理）已知函数
在（0，+∞）上连续，则实数a的值为 ．
【答案】分析：由于当 0＜x＜1时，f（x）=-
，当x≥1时，f（x）=x+a，再根据连续函数的定义可得两段上函数值在端点处相等，由此求得实数a的值．
解答：解：由题意可得，当 0＜x＜1时，f（x）=
+
=
=-
，当x≥1时，f（x）=x+a．
∵函数
在（0，+∞）上连续，∴-
=1+a，解得 a=-
，
故答案为-
．
点评：本题主要考查函数在某处连续的定义，利用分段函数在某处连续时，则两段的函数值在此处相等，属于基础题．
，当x≥1时，f（x）=x+a，再根据连续函数的定义可得两段上函数值在端点处相等，由此求得实数a的值．解答：解：由题意可得，当 0＜x＜1时，f（x）=
+==-，当x≥1时，f（x）=x+a．∵函数
在（0，+∞）上连续，∴-=1+a，解得 a=-，故答案为-
．点评：本题主要考查函数在某处连续的定义，利用分段函数在某处连续时，则两段的函数值在此处相等，属于基础题．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
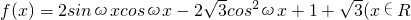，ω＞0）的最小正周期是π．
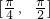上恒成立，求实数m的取值范围．
，ω＞0）的最小正周期是π．
上恒成立，求实数m的取值范围．
在（0，+∞）上连续，则实数a的值为________．