题目内容
(理)已知函数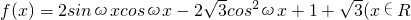 ,ω>0)的最小正周期是π.
,ω>0)的最小正周期是π.
(1)求ω的值;
(2)求函数f(x)的单调增区间;
(3)若不等式|f(x)-m|<2在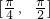 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
解:(理)(1)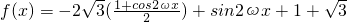 ----(2分)
----(2分)
=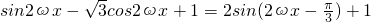 -------(3分)
-------(3分)
由题设可得,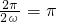 ,所以ω=1.---------------------------(4分)
,所以ω=1.---------------------------(4分)
(2)由(1)得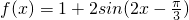 ,由题意
,由题意
则有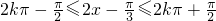 ,(k∈Z)------------(7分)
,(k∈Z)------------(7分)
即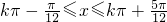 (k∈Z)
(k∈Z)
故 单调增区间为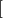 ,(k∈Z)----(10分)
,(k∈Z)----(10分)
(3)∵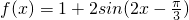 .又∵
.又∵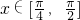 ,∴
,∴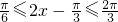 ,------------------------------------------(11分)
,------------------------------------------(11分)
即 ,----------------------------------(13分)
,----------------------------------(13分)
∴f(x)max=3,f(x)min=2.∵|f(x)-m|<2?f(x)-2<m<f(x)+2,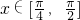 ,---------------------(14分)
,---------------------(14分)
∴m>f(x)max-2,m<f(x)min+2,∴1<m<4,
即m的取值范围是(1,4).---------------------------------------(16分)
分析:(1)求三角函数的周期要先对函数的解析式进行化简,再由公式T= 建立方程求出参数的值;
建立方程求出参数的值;
(2)由(1)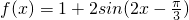 ,令其相位满足
,令其相位满足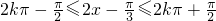 ,k∈Z,解出x的取值范围,即可得到所求的单调增区间;
,k∈Z,解出x的取值范围,即可得到所求的单调增区间;
(3)先解出函数f(x)在区间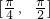 上的最值,由绝对值不等式的性质转化出关于m的不等式,解出其范围即可
上的最值,由绝对值不等式的性质转化出关于m的不等式,解出其范围即可
点评:本题以三角函数为背景考查函数恒成立的问题,函数恒成立的问题是函数中一类难度较高的题型,解答此类题关键是对问题正确转化,此类题一般是求参数范围的题,将恒成立的关系转化为参数所满足的不等式或方程是常规思路,本题考查了转化的思想,方程的思想,变形的能力,推理论证的能力,综合性较强
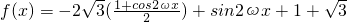 ----(2分)
----(2分)=
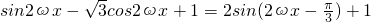 -------(3分)
-------(3分)由题设可得,
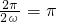 ,所以ω=1.---------------------------(4分)
,所以ω=1.---------------------------(4分)(2)由(1)得
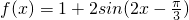 ,由题意
,由题意则有
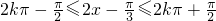 ,(k∈Z)------------(7分)
,(k∈Z)------------(7分)即
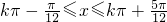 (k∈Z)
(k∈Z)故 单调增区间为
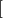 ,(k∈Z)----(10分)
,(k∈Z)----(10分)(3)∵
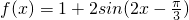 .又∵
.又∵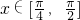 ,∴
,∴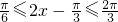 ,------------------------------------------(11分)
,------------------------------------------(11分)即
 ,----------------------------------(13分)
,----------------------------------(13分)∴f(x)max=3,f(x)min=2.∵|f(x)-m|<2?f(x)-2<m<f(x)+2,
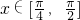 ,---------------------(14分)
,---------------------(14分)∴m>f(x)max-2,m<f(x)min+2,∴1<m<4,
即m的取值范围是(1,4).---------------------------------------(16分)
分析:(1)求三角函数的周期要先对函数的解析式进行化简,再由公式T=
 建立方程求出参数的值;
建立方程求出参数的值;(2)由(1)
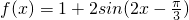 ,令其相位满足
,令其相位满足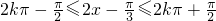 ,k∈Z,解出x的取值范围,即可得到所求的单调增区间;
,k∈Z,解出x的取值范围,即可得到所求的单调增区间;(3)先解出函数f(x)在区间
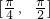 上的最值,由绝对值不等式的性质转化出关于m的不等式,解出其范围即可
上的最值,由绝对值不等式的性质转化出关于m的不等式,解出其范围即可点评:本题以三角函数为背景考查函数恒成立的问题,函数恒成立的问题是函数中一类难度较高的题型,解答此类题关键是对问题正确转化,此类题一般是求参数范围的题,将恒成立的关系转化为参数所满足的不等式或方程是常规思路,本题考查了转化的思想,方程的思想,变形的能力,推理论证的能力,综合性较强

练习册系列答案
相关题目