题目内容
5．设非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足：|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|，$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$，则＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=（ ）| A． | 150° | B． | 120° | C． | 60° | D． | 30° |
分析 设向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$的模长为1，对$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$两边平方得出$\overrightarrow{a}•\overrightarrow{b}$，代入夹角公式得出夹角．
解答 解：设|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|=1，
∵$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$，∴${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}={\overrightarrow{c}}^{2}$，
∴2+2$\overrightarrow{a}•\overrightarrow{b}$=1，解得$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$．
∴cos＜$\overrightarrow{a}，\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{1}{2}$．
∴＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=120°．
故选；B．
点评 本题考查了平面向量的数量积运算，属于中档题．
优惠劵1：若标价超过50元，则付款时减免标价的10%；
优惠劵2：若标价超过100元，则付款时减免20元；
优惠劵3：若标价超过100元，则超过100元的部分减免18%．
若顾客购买某商品后，使用优惠劵1比优惠劵2、优惠劵3减免的都多，则他购买的商品的标价可能为（ ）
| A． | 179元 | B． | 199元 | C． | 219元 | D． | 239元 |
| A． | -$\frac{5π}{6}$ | B． | -$\frac{2π}{3}$ | C． | -$\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
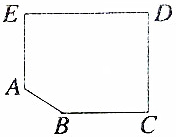某小区内有一块荒地ABCDE，今欲在该荒地上划出一块长方形地面（不改变方位）进行开发（如图所示），问如何设计才能使开发的面积最大？最大开发面积是多少？（已知BC=210m，CD=240m，DE=300m，EA=180m）| A． | a=1，b=1 | B． | a=-1，b=1 | C． | a=1，b=-1 | D． | a=-1，b=-1 |