题目内容
6.已知y=kx+4,定义域为(1,4),求值域.分析 根据函数的单调性进行求解即可.
解答 解:若k=0,则y=4,当1<x<4时,y=4,此时函数的值域为{4},
若k>0,则函数y=kx+4为增函数,当1<x<4时,k+4<y<4k+4,此时函数的值域为[k+4,4k+4],
若k<0,则函数y=kx+4为减函数,当1<x<4时,4k+4<y<k+4,此时函数的值域为[4k+4,k+4].
点评 本题主要考查函数值域的求解,根据k的取值范围,结合函数的单调性的性质是解决本题的关键.

练习册系列答案
相关题目
16.设A,B,C,D是空间中的四个不同的点,则下列说法错误的是( )
| A. | 若AC与BD共面,则AD与BC也共面 | |
| B. | 若AC与BD是异面直线,则AD与BC也是异面直线 | |
| C. | 若AC与BD是相交直线,则AD与BC也是相交直线 | |
| D. | 若A,B,C,D不共面,则AC与BD既不平行也不相交 |
14.经过同一直线上的3个点的平面( )
| A. | 有且只有一个 | B. | 有且只有3个 | C. | 有无数个 | D. | 不存在 |
16.设M={x|0≤x≤2},N={y|0≤y≤2},给出如图所示的四个图形:
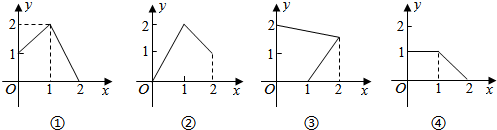
其中能表示从集合M到集合N的函数关系式的有( )

其中能表示从集合M到集合N的函数关系式的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |