Question

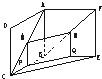
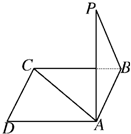
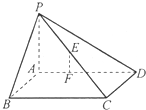
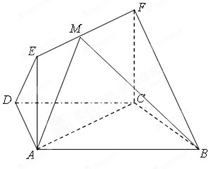
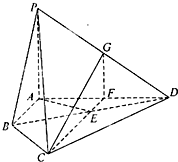
如图，四棱锥P-ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点△DAB≌△DCB，EA=EB=AB=1，PA=

3

2

，连接CE并延长交AD于F．
（1）求证：AD⊥平面CFG；
（2）求三棱锥P-ABD外接球的体积．

Answer 1

（1）在△ABD中，∵E是BD的中点，
∴EA=EB=ED=AB=1，∴AE=

1

2

BD，
可得∠BAD=

π

2

，且∠ABE=∠AEB=

π

3

，
∵△DAB≌△DCB，
∴△EAB≌△ECB，
从而有∠FED=∠FEA=∠AEB=

π

3

，
故EF⊥AD，AF=FD，
又∵△PAD，中，PG=GD，
∴FG是△PAD的中位线，
∴FG∥PA．
又PA⊥平面ABCD，
∴FG⊥平面ABCD，
∵AD?平面ABCD，
∴GF⊥AD，
又∵EF，FG是平面CFG内的相交直线，
∴AD⊥平面CFG．
（2）∵PA、PB、PD两两垂直，可补形成长方体，
其外接球2R=

12+( 3 )2+( 3 2 )2

=

5

2

，
∴R=

5

4

，
∴V=

4

3

πR3=

125π

48

．