题目内容
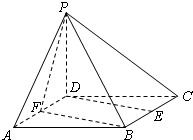
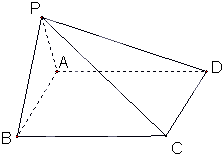
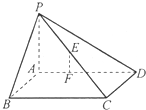
（理）如图，四棱锥P-ABCD的底面是矩形，PA⊥面ABCD，PA=2
，AB=8，BC=6，点E是PC的中点，F在AD上且AF：FD=1：2．建立适当坐标系．
（1）求EF的长；
（2）证明：EF⊥PC．
| 19 |
（1）求EF的长；
（2）证明：EF⊥PC．
（1）以A为原点，
，
，
分别为x，y，z轴建立直角坐标系，
由条件知：AF=2，
∴F（0，2，0），P（0，0，2
），C（8，6，0），从而E（4，3，
），
∴EF=
=6．
（2）证明：
=（-4，-1，-
），
=（8，6，-2
），
∵
•
=-4×8+（-1）×6+（-
）×（-2
）=0，
∴EF⊥PC．
| AB |
| AD |
| AP |
由条件知：AF=2，
∴F（0，2，0），P（0，0，2
| 19 |
| 19 |
∴EF=
(4-0)2+(3-2)2+(
|
（2）证明：
| EF |
| 19 |
| PC |
| 19 |
∵
| EF |
| PC |
| 19 |
| 19 |
∴EF⊥PC．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
