题目内容
已知动点P(p,-1),Q(p,1+| p2 |
| 2 |
| p |
| 2 |
(1)证明:l经过一个定点而且与曲线C一定有两个公共点;
(2)若(1)中的其中一个公共点为A,证明:AP是曲线C的切线.
分析:(1)先用消参法求出P Q中点M的轨迹方程,再求出带参数p的直线l的方程,与点M的轨迹方程联立,再判断△的大小,即可得到直线l与曲线C一定有两个公共点,
(2)先解(1)中联立方程组得到的一元二次方程,得到A点坐标,利用斜率公式求出AP的斜率,再用导数求出斜率,观察两者是否相等,即可得证.
(2)先解(1)中联立方程组得到的一元二次方程,得到A点坐标,利用斜率公式求出AP的斜率,再用导数求出斜率,观察两者是否相等,即可得证.
解答:解:(1)直线l的方程是:y-1-
=
(x-p),即y=
x+1,经过定点(0,1);
又M(p,
),设x=p,y=
,消去p,得到的轨迹方程为:y=
.
由
有x2-2px-4=0,其中△=4p2+16,所以l经过一个定点而且与曲线C一定有两个公共点
(2)由x2-2px-4=0,设A(p+
,
),
则kAP=
=
,
又函数y=
的导函数为y=
,故A处的切线的斜率也是
,从而AP是曲线C的切线.对于另一个解同样可证.
| p2 |
| 2 |
| p |
| 2 |
| p |
| 2 |
又M(p,
| p2 |
| 4 |
| p2 |
| 4 |
| x2 |
| 4 |
由
|
(2)由x2-2px-4=0,设A(p+
| p2+4 |
(p+
| ||
| 4 |
则kAP=
| ||||
|
p+
| ||
| 2 |
又函数y=
| x2 |
| 4 |
| x |
| 2 |
p+
| ||
| 2 |
点评:本题考查了直线与圆锥曲线的关系,特别是相交和相切关系,巧妙地利用韦达定理,导数的几何意义可有效提高解题速度

练习册系列答案
相关题目
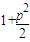 ),过Q作斜率为
),过Q作斜率为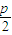 的直线l,P Q中点M的轨迹为曲线C.
的直线l,P Q中点M的轨迹为曲线C.