题目内容
若函数y=2tanωx的最小正周期为2π，则函数y=sin
的最小正周期为________．
4π
分析：利用函数y=2tanωx的最小正周期为2π，求出ω，然后化简函数的表达式，利用周期公式求出函数的周期即可．
解答：因为函数y=2tanωx的最小正周期为2π，所以ω=
=
，
所以函数y=sin=2sin（x+
）的最小正周期T=
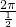=4π．
故答案为：4π．
点评：本题考查三角函数的周期的应用，两角和的正弦函数的应用，考查计算能力．
分析：利用函数y=2tanωx的最小正周期为2π，求出ω，然后化简函数的表达式，利用周期公式求出函数的周期即可．
解答：因为函数y=2tanωx的最小正周期为2π，所以ω=
=，所以函数y=sin
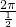=2sin（x+）的最小正周期T==4π．故答案为：4π．
点评：本题考查三角函数的周期的应用，两角和的正弦函数的应用，考查计算能力．
练习册系列答案
相关题目
的最小正周期为 ．
的最小正周期为 ．