题目内容
各项都是正数的等比数列{an}中,a2, a3,a1成等差数列,则
a3,a1成等差数列,则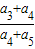 的值是( )
的值是( )A.
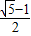
B.
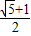
C.
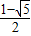
D.
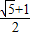 或
或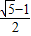
【答案】分析:由a2, a3,a1成等差数列可得a1、a2、a3的关系,结合等比数列的通项公式即可求出q,而由等比数列的性质可得 则
a3,a1成等差数列可得a1、a2、a3的关系,结合等比数列的通项公式即可求出q,而由等比数列的性质可得 则 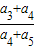 =
=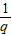 ,故本题得解.
,故本题得解.
解答:解:设{an}的公比为q(q>0),
由a3=a2+a1,得q2-q-1=0,
解得q=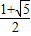 .
.
∴则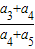 =
=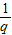 =
=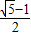 .
.
故答案为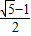 .
.
点评:此题考查学生灵活运用等差数列的性质及等比数列的性质化简求值,灵活运用等比数列的通项公式化简求值,是一道基础题.
 a3,a1成等差数列可得a1、a2、a3的关系,结合等比数列的通项公式即可求出q,而由等比数列的性质可得 则
a3,a1成等差数列可得a1、a2、a3的关系,结合等比数列的通项公式即可求出q,而由等比数列的性质可得 则 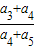 =
=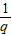 ,故本题得解.
,故本题得解.解答:解:设{an}的公比为q(q>0),
由a3=a2+a1,得q2-q-1=0,
解得q=
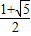 .
.∴则
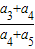 =
=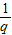 =
=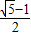 .
.故答案为
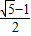 .
.点评:此题考查学生灵活运用等差数列的性质及等比数列的性质化简求值,灵活运用等比数列的通项公式化简求值,是一道基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
设Sn是各项都是正数的等比数列{an} 的前n项和,若
≤Sn+1,则公比q的取值范围是( )
| Sn+Sn+2 |
| 2 |
| A、q>0 |
| B、0<q≤1 |
| C、0<q<1 |
| D、0<q<1或q>1 |