题目内容
20.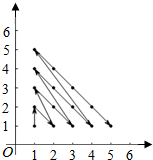 已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )
已知整数按如下规律排成一列:(1,1)、(1,2)、(2,1)、(1,3)、(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第70个数对是( )| A. | (2,11) | B. | (3,10) | C. | (4,9) | D. | (5,8) |
分析 由已知可知:其点列的排列规律是(m,n)(m,n∈N*)m+n的和从2开始,依次是3,4…增大,其中m也是依次增大.据此即可得出.
解答 解:由已知可知:其点列的排列规律是(m,n)(m,n∈N*)m+n的和从2开始,依次是3,4…增大,其中m也是依次增大.
而m+n=2只有一个(1,1);
m+n=3有两个(1,2),(2,1);
m+n=4有3个(1,3),(2,2),(3,1);
…
m+n=11有10个(1,10),(2,9),…,(10,1);
m+n=12有11个(1,11),(2,10),…,(11,1);
其上面共有1+2+…+11=66个;
m+n=13的有(1,12),(2,11),(3,10),(4,9),(5,8),(6,7),(7,6)…
故第70个数对是(4,9).
故选:C
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
10.在半径为8cm的圆中,$\frac{5π}{3}$的圆心角所对的弧长( )
| A. | $\frac{400π}{3}cm$ | B. | $\frac{20π}{3}cm$ | C. | $\frac{200π}{3}cm$ | D. | $\frac{40π}{3}cm$ |
11.由1,2,3,4,5,6等6个数可组成( )个无重复且是6的倍数的5位数.
| A. | 100 | B. | 120 | C. | 240 | D. | 300 |
12.确定结论“X与Y有关系”的可信度为99.5%时,则随即变量k2的观测值k必须( )
| A. | 大于10.828 | B. | 大于7.879 | C. | 小于6.635 | D. | 大于2.706 |
9.某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有( )
| A. | 474种 | B. | 77种 | C. | 464种 | D. | 79种 |
10.在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
通过计算得到回归方程为$\stackrel{∧}{y}$=0.577x-0.448,利用这个方程,我们得到年龄37岁时体内脂肪含量为20.90%,那么数据20.90%的意义是( )
| 年龄 | 23 | 27 | 39 | 41 | 45 | 49 | 50 | 53 | 56 | 58 | 60 |
| 脂肪 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 26.3 | 28.2 | 29.6 | 31.4 | 33.5 | 35.2 |
| A. | 某人年龄37岁,他体内脂肪含量为20.90% | |
| B. | 某人年龄37岁,他体内脂肪含量为20.90%的概率最大 | |
| C. | 某人年龄37岁,他体内脂肪含量的期望值为20.90% | |
| D. | 20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计 |