题目内容
5．函数y=cosx|tanx|（-$\frac{π}{2}$＜x＜$\frac{π}{2}}$）的大致图象是（ ）| A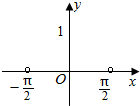． |  | B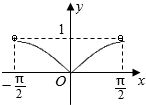． |  | C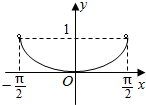． |  | D． |  |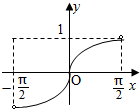
分析 化简函数的解析式，然后判断函数的图象即可．
解答 解：-$\frac{π}{2}$＜x＜$\frac{π}{2}}$⇒cosx＞0，故函数y=cosx|tanx|=|sinx|，
函数y=cosx|tanx|（-$\frac{π}{2}$＜x＜$\frac{π}{2}}$）的大致图象是：B．
故选：B．
点评 本题考查三角函数的化简，函数的图象的判断，考查计算能力．
练习册系列答案
相关题目
20．
已知整数按如下规律排成一列：（1，1）、（1，2）、（2，1）、（1，3）、（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…，则第70个数对是（ ）
已知整数按如下规律排成一列：（1，1）、（1，2）、（2，1）、（1，3）、（2，2），（3，1），（1，4），（2，3），（3，2），（4，1），…，则第70个数对是（ ）| A． | （2，11） | B． | （3，10） | C． | （4，9） | D． | （5，8） |
某工程设计一条单行隧道，其横截面如图所示，下部ABCD为长8米高2米的矩形，上部$\widehat{CED}$是圆弧的一部分，欲使宽6米高3米的大型货车刚好能通过，求拱顶E距离路面AB至少需几米？
17．设复数$Z=lg（{{m^2}-1}）+{\sqrt{1-m}_{\;}}i$，Z在复平面内的对应点（ ）
| A． | 一定不在一、二象限 | B． | 一定不在二、三象限 | ||
| C． | 一定不在三、四象限 | D． | 一定不在二、三、四象限 |
14．函数f（x）的定义域为R，f（0）=2，对任意x∈R，f（x）+f′（x）＞1，则不等式exf（x）＞ex+1，的解集是（ ）
| A． | {x|x＞0} | B． | {x|x＜0} | C． | {x|x＜-1或x＞1} | D． | {x|-1＜x＜1 } |