Question

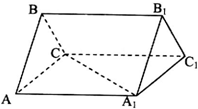（2012•威海一模）如图三棱柱ABC-A₁B₁C₁中，底面ABC⊥侧面AA₁C₁C，△AA₁C为等边三角形，AB⊥BC且AB=BC，三棱锥B-AA₁C的体积为

9 3

8

．
（I）求证：AC⊥A₁B；
（II）求直线A₁C与平面BAA₁所成角的正弦值．

Answer 1

分析：（Ⅰ）取AC中点为O，利用线面垂直的判定定理证明AC⊥平面BOA₁，即可证明AC⊥A₁B；
（Ⅱ）建立空间直角坐标系，求出平面A₁AB的法向量，利用向量的夹角公式，即可求直线A₁C与平面A₁AB所成角的正弦值．

解答：（I）证明：取AC中点为O，
∵AB=BC，∴BO⊥AC
∵△AA₁C为等边三角形，∴OA₁⊥AC
∵OA₁∩BO=O
∴AC⊥平面BOA₁，
∴AC⊥A₁B；
（II）解：设AC=a，则有

1

3

•

3

4

a2•

1

2

a=

9 3

8

，∴a=3
建立如图所示的空间直角坐标系，则C（0，

3

2

，0），A1(

3 3

2

，0，0)，A(0，-

3

2

，0)，B(0，0，

3

2

)

A1C

=(-

3 3

2

，

3

2

，0)，

AB

=(0，

3

2

，

3

2

)，

AA1

=(

3 3

2

，

3

2

，0)

设平面A₁AB的法向量为

n

=（x，y，1），则由

n • AB =0 n • AA1 =0

可得

3 2 y+ 3 2 =0 3 3 2 x+ 3 2 y=0

，∴

x= 3 3 y=-1

，∴

n

=(

3

3

，-1，1)
∴cos＜

n

，

A1C

＞=

n • A1C

| n || A1C |

=-

21

7

∵直线A₁C与平面A₁AB所成角θ和向量

n

与

A1C

所成锐角互余，
∴直线A₁C与平面BAA₁所成角的正弦值为

21

7

．

点评：本小题主要考查空间线面关系、直线与平面所成的角、三角函数等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．