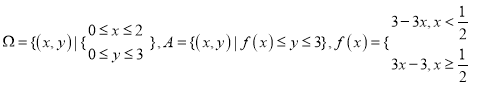题目内容
【题目】已知椭圆![]() ,与
,与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,右焦点
,右焦点![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() .
.
(1)求椭圆的离心率![]() ;
;
(2)已知点![]() ,过点
,过点![]() 任意作直线
任意作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,设直线
两点,设直线![]() 的斜率
的斜率![]() ,若
,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)tan∠PFO=![]() 可得
可得![]() =
=![]() ,c=
,c=![]() b,a=
b,a=![]() =
=![]() b即可得出(2)直线斜率不为0时,设出直线方程ty=x﹣1,设C(x1,y1),D(x2,y2).联立
b即可得出(2)直线斜率不为0时,设出直线方程ty=x﹣1,设C(x1,y1),D(x2,y2).联立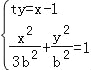 ,化为:(t2+3)y2+2ty+1﹣3b2=0,∵k1+k2=2,∴
,化为:(t2+3)y2+2ty+1﹣3b2=0,∵k1+k2=2,∴![]() +
+![]() =2,根据韦达定理代入求解即可,斜率为0 时也成立
=2,根据韦达定理代入求解即可,斜率为0 时也成立
试题解析:
(1)∵tan∠PFO=![]() ,∴
,∴![]() =
=![]() ,∴c=
,∴c=![]() b,a=
b,a=![]() =
=![]() b.
b.
∴![]() =
=![]() =
=![]() .
.
(2)直线l的斜率不为0时,设直线l的方程为:ty=x﹣1.设C(x1,y1),D(x2,y2).
联立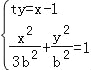 ,化为:(t2+3)y2+2ty+1﹣3b2=0,
,化为:(t2+3)y2+2ty+1﹣3b2=0,
y1+y2=![]() ,y1y2=
,y1y2=![]() ,
,
∵k1+k2=2,∴![]() +
+![]() =2,
=2,
化为:(y1﹣2)(ty2﹣2)+(y2﹣2)(ty1﹣2)=2(ty1﹣2)(ty2﹣2),
即:ty1y2=y1+y2,
∴t![]() =
=![]() ,对t∈R都成立.
,对t∈R都成立.
化为:b2=1,
直线l的斜率为0时也成立,
∴b2=1,
∴椭圆C的方程为![]() .
.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目